程式碼的時間複雜度是評估程式執行時間所需的操作數或步驟數。它以 Big O 符號表示，代表算法執行時間隨著輸入大小增長的速度。較低的時間複雜度通常表示更好的效能。我們分析程式碼中的迴圈、條件語句和遞迴等關鍵部分，根據其執行次數來評估效率。例如，一個遍歷n個元素的迴圈的時間複雜度為O(n)。通過分析時間複雜度，我們可以比較不同算法或程式碼片段的效率，以選擇最佳解決方案。然而，時間複雜度僅為理論估計，實際執行時間受多種因素影響。
程式碼的時間複雜度，在沒有輔助工具的情況下，多數只能靠人工自行估算，而現在我們可以透過「TimeComplexity.ai」這個網站，使用者僅需貼上程式碼片段，就可以使用 AI 來估算，並且說明估算原則及其步驟，至於準確度如何呢？網站有提供資料結構上常用的教學範例，也是考試非常愛考的題目，像是 evenOdd()、maxSubArray()、binarySearch()、mergeSort()、bubbleSort()及 threeSum() 倒是滿符合的。
使用「TimeComplexity.ai」網站來估算程式碼的時間複雜度，未註冊用戶有每日20次的使用限制，註冊用戶為 50次，超過這些次數可以付費。
如何使用 TimeComplexity.ai 估算程式碼時間複雜度？
1.想要知道在 TimeComplexity.ai 網站上使用 AI 估算程式碼時間複雜度的準確性，網站自己有準備了，像是 evenOdd()、maxSubArray()、binarySearch()、mergeSort()、bubbleSort() 以及 threeSum()這些有標準答案的範例。
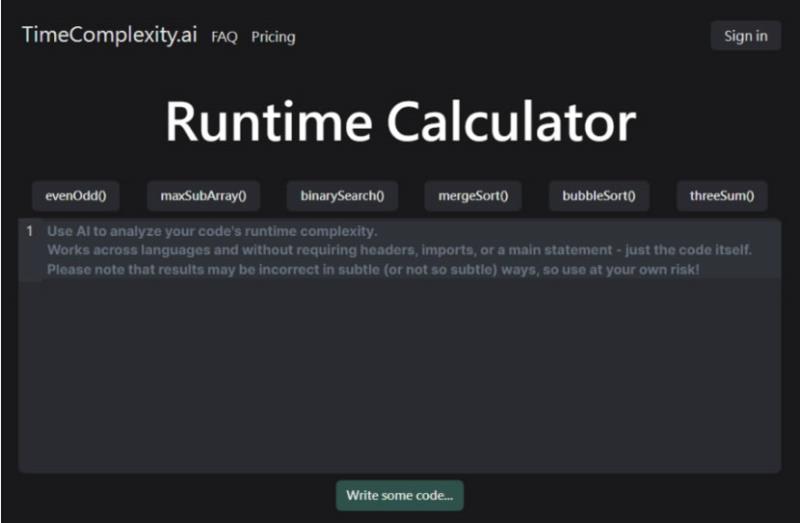
2.就 binarySearch() 來看，除了有程式碼還會有估算說明。
3.二分搜尋法，可參考：維基百科 - Wikipedia